
The result p is the probability that a single observation from a gamma distribution with parameters a and b falls in the interval 0, x. Note that a 0 corresponds to the trivial distribution with all mass at point 0. 7 6 21:37 30 years old level / A student / Very /. Comment/Request Very interesting The only thing I would like to have here that is not available would be the parameters of the scale of the y axis. Then we dive into the mathematical background and introduce the formulas. Nunung Nurhayati Teori Peluang (PAM 2231)-Unsoed 3. Analyzing the shape of the gamma distribution to use as a prior for estimating the parameter of a poisson distribution. (Here Gamma(a) is the function implemented by R s gamma() and defined in its help. We build an intuitive understanding of the Gamma distribution by going through some practical examples. Let Tdenote the length of time until the rst arrival. Relation of Poisson and exponential distribution: Suppose that events occur in time according to a Poisson process with parameter. The Gamma distribution with parameters shape a and scale s has density. Poisson, Gamma, and Exponential distributions A. Is this reasoning technically correct? I would highly appreciate if anyone could suggest a different method. p F ( x a, b) 1 b a ( a) 0 x t a 1 e t b d t. If scale is omitted, it assumes the default value of 1.
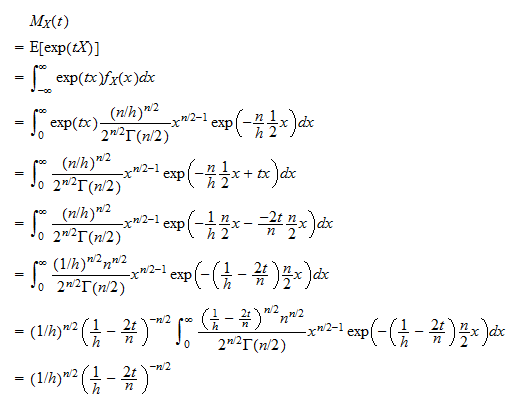
( Note: there is a slight difference on how I have defined the scale parameter and how it is given on the Wikipedia page)į_x(x n, \lambda) = \fracįinally, subtracting the above value from $1$ gives us the CDF in the required form. Gamma distribution functions PDFGamma( x, a, b ) PDFGamma( x, a, b ) returns the probability density at the value x of the Gamma distribution with parameters a and b. I found the following result on Wikipedia relating to the CDF of the Gamma Distribution when the shape parameter is an integer.


 0 kommentar(er)
0 kommentar(er)
